圧力・体積・温度の関係〜ダイビングとボイル・シャルルの法則〜

コンビニでホットドッグを買ってレンジで温めてもらう時、店員さんはおもむろに袋の端を切って封を開けますよね。
お客様が購入した商品を勝手に開けるだなんて……。

温めもしないポテチの袋を勝手に開けられたら皆さん怒ることでしょうが、レンジで温める前にホットドッグの袋を勝手に開けられても怒る人はいませんよね。
それは経験則的に、封をしたまま温めてしまうと、袋が爆発してしまうことを知っているからではないでしょうか。

ではなぜ、レンジでホットドッグの封を開けずに温めると爆発してしまうのでしょうか。

結論から言えば、温めると袋の内部の空気が膨張するためですが、この様に気体の大きさが変化するという現象にはダイビングにも密接に関りがあります。

気体は膨らみ、しぼむ

世の中に存在する様々な物質は、常に同じ大きさでしょうか。
ほとんどの物の大きさは通常変化しませんよね。

力を加えれば形を変えたり壊れたりすることはあっても、人間が力を加えたぐらいで大きさが変化する物はあまりありません。

しかし、物質は力や熱を加えられることで確実に大きさが変化します。
身の回りの多くを占める固体や液体の場合、その変化が非常に小さいため、変化していない様に感じるだけです。

たとえば、電車に乗った時のことを思い出してみましょう。
電車遊びの掛け声といえば「ガタンゴトン」ですが、その通りの音がしますよね。
これは、レールのつなぎ目に隙間があるため、そこを車輪が通過する際にガタゴトと音を立てています。

レールをピッタリとくっつけて設置すれば音はほとんど出ないのに、なぜわざわざレールのつなぎ目には隙間があるのでしょうか。

電車のレールは金属でできていますが、金属（に限らずほとんどの物質）は温められると膨張し、冷やされると収縮します。
はじめからピッタリとくっつけてレールを設置してしまうと、夏の暑い時期には設置時よりもレールが膨張し、レールが曲がるなどの不具合を起こしてしまいます。

そうならない様に、はじめから夏にレールが膨張する事を計算に入れて、隙間を開けて設置しているのです。
同様に、コンクリートで出来た大きな橋や高架なども、敢えて隙間を開けて作られています。
車で橋や高架を通った際、道路全体を横切る黒いゴムの様な物があれば、その部分がつなぎ目で、隙間が開いています。

この様に、様々な物質は外部から熱や力が加わると大きさが変化するのですが、空気をはじめとした気体の場合は、冒頭のホットドッグの様に、少しの熱や力でもすぐに大きさを変化させます。
ホットドッグ内の空気がレンジによって温められると膨張し、最終的には袋がその空気の大きさに耐えきれずに爆発してしまうわけですね。

どれぐらい変化するの？

では、ホットドッグの袋は何度まで温められると爆発してしまうのでしょうか。
袋の強度にもよるので実際に計算することはしませんが、空気がどれだけ温められたらどれだけ膨張するのかは、簡単に計算することができます。

例えば27℃の場所に風船があるとしましょう。
この風船をアツアツのサウナ、103℃の場所に持っていくと、その大きさは約1.3倍（4/3倍）になります。

計算方法は後段でご説明しますが、気体には熱や力による大きさの変化を簡単な計算で求められるという特性があります。
一方、風船の中身が水などの液体や金属などの個体の場合、計算は非常に複雑になります。

熱、力、大きさ、という言葉を使用してきましたが、力とは圧力の事、大きさとは体積の事です。
圧力というダイビングに関係がありそうな言葉が出てきたところで、ここまでダイビングからは離れた例ばかりでしたが、いよいよダイビングを例にとってみましょう。

• エントリー前に残圧を確認した時には200気圧あったはずなのに、エントリー後、まだ潜降しておらず一呼吸もしていないのに、残圧が減っていたという経験はありませんか？
• 誤ってタンクのバルブを思いっきり開いた際、バルブ周辺が冷たくなっていたという経験はありませんか？
• 器材のカタログで、寒冷地使用レギュレーターという様な言葉を見たことはありませんか？

これらは全て、これからご紹介する法則によって説明することができます。

気体の変化の法則

気体の変化の法則は非常にシンプルです。

（圧力）×（体積）÷（温度）は常に一定

これが気体の変化に関する法則です。

法則らしく書くのであれば、以下の通り。

この法則をボイル・シャルルの法則と言います。

この法則の何が凄いかって、どんな気体でも、たとえ複数の気体が混ざっていても、同じことが当てはまるのです。
酸素だろうと、二酸化炭素だろうと、空気だろうと、です。
液体や固体は物質によって変化率が異なるため、こんなに単純な話ではありません。

実際の現象

（圧力）×（体積）÷（温度）が一定なので、どれかひとつの値が固定されると、残る二つの関係は比例するか、反比例するかの、シンプルな関係性となります。

温度一定の場合

温度が一定の場合、圧力と体積は反比例の関係にあります。
つまり、圧力が上がれば体積は減り、圧力が下がれば体積は増えるということですね。
逆に、体積を増やせば圧力は下がり、体積を減らせば圧力は増えます。

どこかで聞いたことはありませんか？

水圧と体積の関係は反比例しますが、なぜ反比例するのかまでは踏みこまず、天下り式に教わることも多いかと思います。
この圧力と体積が反比例するというのは気体の法則そのものだったんですね。

圧力と体積の関係

尚、温度一定の状態で圧力と体積が反比例するということだけを指してボイルの法則と呼ぶこともあります。

圧力一定の場合

圧力が一定の場合、体積と温度は比例の関係にあります。
つまり、温度が上がれば体積も増え、温度が下がれば体積も減ります。
逆に、体積が増えれば温度も上がり、体積が減れば温度も下がります。

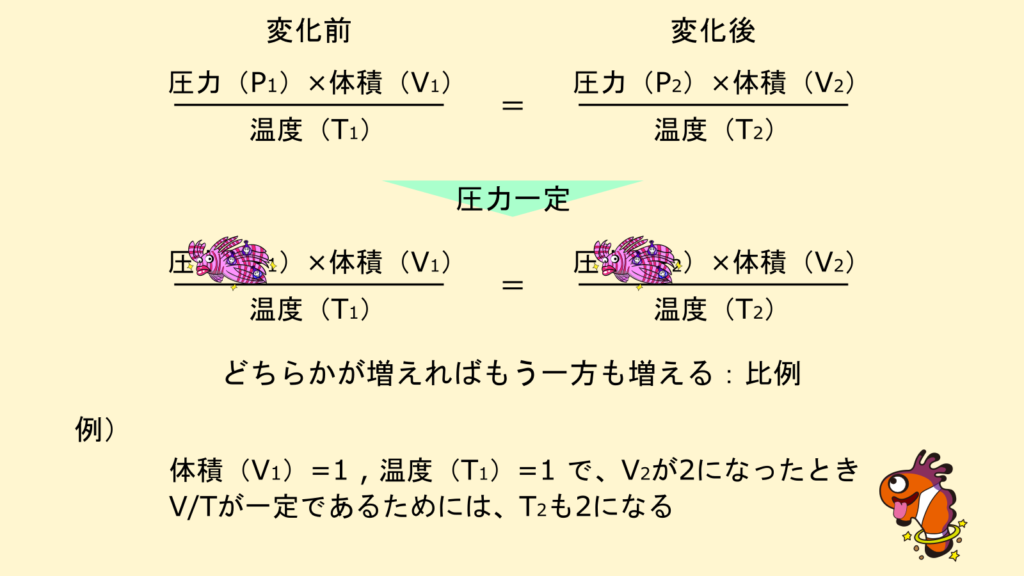
冒頭のホットドックの例が、これに当てはまりますね。

尚、圧力一定の状態で体積と温度が比例するということだけを指してシャルル（シャール）の法則と呼ぶこともあります。

体積一定の場合

体積が一定の場合、圧力と温度は比例の関係にあります。
つまり、温度が上がれば圧力も増え、温度が下がれば圧力も減ります。
逆に、圧力が上がれば温度も上がり、圧力が下がれば温度も下がります。

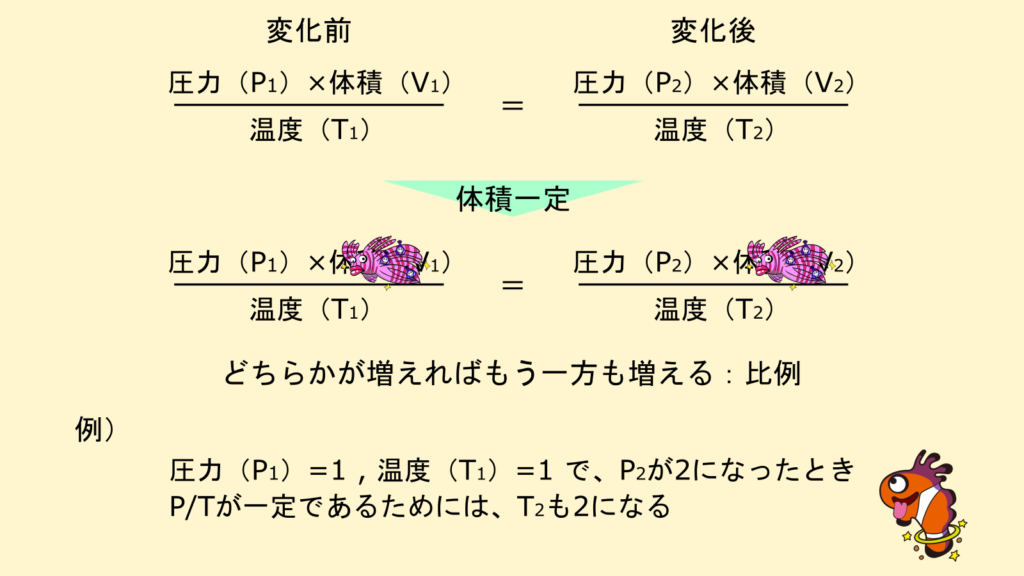
タンクに空気を充填する際、タンクの体積は一定で、圧力が上がります。
そのため、充填直後のタンクは周囲の温度よりも温まっています。

真夏などでタンクが日光によって温められている場合、エントリー前に200気圧あった残圧も、エントリーしてタンクが冷やされることで温度の変化に比例して減ることになります。

レギュレーターには寒冷地対応のものとそうでないものがありますが、レギュレーターで呼吸を行うと、体積一定で圧力が低下します。
すると、温度も下がります。
このとき周囲の温度が0℃に近い場合、それよりも低い温度に下がってしまうために、レギュレーター内部の水滴などが凍ってしまい、レギュレーターが故障してしまいます。

これらは全て、体積一定の場合で説明することができます。

ちなみに寒冷地対応のレギュレーターは、上記の凍結への対策が行われているレギュレーターということです。

尚、体積一定の状態で圧力と温度が比例するということだけを指してアモントンの法則、またはゲイ＝リュサックの法則と呼ぶこともあります。

実際に計算してみよう

実際に計算を行う場合、ひとつだけ注意点があります。

圧力と体積については、どんな単位を使用しても構いません。
圧力であれば気圧（atm）でもbarでもhPaでもなんでもOK。
体積であれば㎥でも㎤でもℓでもなんでもOKです。

ただし、温度だけは必ずK（ケルビン）という単位を使用します。
聞きなれない単位かもしれませんが、絶対温度という単位です。

ではどうやって計算するかと言えば、普段使用する℃に273を足すだけでOKです。
つまり、0℃なら273K、27℃なら300Kです。
（ボイル・シャルルの法則を用いる計算問題で27℃や1の位が7の数字の温度が頻出するのはこのためです）
尚、厳密には0℃は273.15Kなので273.15を足すべきですが、専門的で厳密な計算以外では、273が使用されることがほとんどです。

実際に計算してみましょう。

太陽に温められ、内部の空気まで37℃になった10ℓタンクがあり、残圧は200気圧だったとします。
このタンクを水温17℃のプールで冷やし、内部の空気まで17℃になった時に残圧を計ると、どのようになるでしょう？

変化の前と後で（圧力）×（体積）÷（温度）が一定なので

200気圧×10ℓ÷（37 + 273）K＝？気圧×10ℓ÷（17 + 273）K

となります。

10ℓは変わらないので両辺から削除し、？を求める式に変換すると

？＝200÷310×290

となり、約187気圧という答えが出ます。

応用編：コンプレッサー問題

ボイル・シャルルの法則を使用する計算問題の集大成として、地上からコンプレッサーで水中に空気を送り込む場合の事を考える問題があります。

水中にある容器に空気を送り込むだなんて、レジャーダイビングの世界では縁の無い話ですが、作業潜水などではあり得るシチュエーション。
そのため、アマチュアダイバーの問題で出てくることは無いと思いますが、プロレベルや国家資格である潜水士の問題には頻出なので、最後に解き方を解説してみたいと思います。

＜問題＞
気温25℃のとき、毎分1000ℓの送気量のコンプレッサーで、水温20℃、水深30mの海底にある容積9500ℓの容器に空気を送り、満たしたい。
この時、容器は何分で満たされるか。

＜方針＞
水中の容器に毎分何ℓずつ送気できるのかを考える

＜答案＞

地上は1気圧、水深30mは4気圧なので

（1気圧×1000ℓ）/｛（25℃+273）K｝＝（4気圧×？ℓ）/｛（20℃＋273）K｝

整理すると

（1気圧×1000ℓ）/298K＝（4気圧×？ℓ）/293K

右辺の数値を左辺に移項すると

（1気圧×1000ℓ×293K）/（298K×4気圧）＝？ℓ

これを計算すると、毎分245.81ℓ（小数第3位で四捨五入）送気できることがわかります。

あとは容器の容積9500ℓをこの数字で割ってあげると

約38.6分でこの容器は満たされるという答えが出てきます。

多くの問題では温度や圧力などどれかひとつの値が固定されているため、比例や反比例の概念だけで解くことができますが、コンプレッサーの問題では3つの数値すべてが変化します。
そのため一見複雑な様に見えますが、（圧力）×（体積）÷（温度）が一定ということを理解していれば、数字を当てはめるだけで簡単に解くことができますよ！

おわりに

必ずしもダイバー全員がコンプレッサーの問題の様な計算問題を解ける様になる必要はありません。
しかし、ここまでご紹介してきた通り、気体の圧力、体積、温度の関係はダイビングにおける様々な減少に深く関わっています。

これまで、圧力と体積は反比例、圧力と温度は反比例、体積と温度も反比例、と別々に覚えていた方もいるかもしれませんが、（圧力）×（体積）÷（温度）が一定という1つの式だけを覚えておけば、ありとあらゆる問題に対応することができるので、こちらを覚えておくと良いでしょう。

アルファベットでPV/T＝一定と覚えた方が覚えやすいかもしれませんね。

それぞれのアルファベットが何を表すのかがわからなくなったとしても、それぞれの英単語の頭文字なので、思い出すことができるのではないでしょうか。

P：Pressure
V：Volume
T：Temperature

です。

ひとつだけ注意点があるとすれば、それぞれの法則の名前を問われたときです。

計算問題を解く上では、PV/T＝一定：ボイル・シャルルの法則だけ覚えておけば十分なのですが、この法則を分割したPV＝一定、P/T＝一定、V/T＝一定、それぞれの法則の名前に関しては覚えるしかありません……。

ちなみに筆者は

ボイル：茹でる＝熱→温度を固定したPV＝一定がボイルの法則。

シャルル：残る二つの法則のうち、ボイル・シャルルの名前に入っているので実生活に馴染みがある現象→実生活で圧力が変化する現象はあまりない→圧力を固定したV/T＝一定がシャルルの法則

アモントン（ゲイ＝リュサック）：残りひとつであるP/T＝一定がアモントンの法則

と覚えています。
とても覚えづらいです。（笑）

何か語呂合わせなどがあれば良いのですが……。
良い語呂合わせなどをご存知の方がいらっしゃいましたら、是非教えてくださいね！